Momentum and Kinetic Energy
Momentum: In physics, the property or tendency of a moving object to continue moving. For an object moving in a line, the momentum is the mass of the object multiplied by its velocity (linear momentum). Thus, a slowly moving very massive body and a rapidly moving, light body can have the same momentum.
Kinetic energy: In physics, kinetic energy of an object is the energy that it possesses due to its motion. It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless it’s speed changes. The
same amount of work is done by the body in deceleration from its current speed to a state of rest.
The Laws of Physics
Force = mass x acceleration. (F= ma)
Mass = slug. (weight divided by the acceleration of gravity)
Acceleration of gravity (g) = 32.174 ft/s²
Velocity = the distance traveled divided by the time elapsed.
Weight = is the force exerted on a body by gravity
Unit of measurement for momentum = slug-ft/s
Unit of measurement for kinetic energy = ft-lb.
7,000 grains =1lb.
When we look at weight vs mass we need to understand they are not the same. Weight will change depending on gravity. This means what you weigh here on earth will not be the same on the moon or Jupiter. But mass will be the same no matter where you are.
How do we calculate momentum?
Mass x velocity = momentum
Weight/g x FPS =slug-ft/s
So first we have to get the mass of the arrow expressed in slugs. To get slugs we need to convert the arrow weight in grains to lb. and then divide by gravity. We know 7000 grains equal to 1lb. So for an example, let’s use numbers from my APA m5. A 429 gr. arrow flying at 287 fps.
grains/1lb./32.174 ft/sec² = slug
429/7000 = 0.0613 lbs
0.0613/32.174 = 0.00190 slugs of mass
Now we have slugs of arrow mass. Let’s figure for slug-ft/s for momentum.
0.0613/32.174 x 287 = 0.547 slug-ft/s
Now from the same bow a 628 gr. arrow at 244 fps.
628/7000 = 0.0897 lbs
0.0897/32.174 = 0.00279 slugs of mass
Now we have slugs of arrow mass. Let’s figure for slug-ft/s for momentum.
.0897/32.174 x 244 = 0.680 slug-ft/s
Let’s look at kinetic energy and how to calculate it.
0.5 x m x v²=k.e.
Using this formula we must convert grains to kilograms for mass and convert fps to meter/second for velocity, and k.e. will be given in joules.
- To convert grains to kilograms = divide grains by 15432 grains to get kg
- To convert fps to m/s. = multiply fps by .305 to get m/s
- To convert joules to k.e. = multiply joules by .738 to get ft lb.
Using the same arrow at 429 gr. at 287 fps
429/15432 = 0.027 kilogram
287 x 0.305 = 87.54 m/s
With the arrow weight and fps converted we now can solve for k.e.
0.5 x 0.027 x 87.54² = 103.45 Joules
103.45 x 0.738 = Ke
Ke =76.34 ft lbs
Using the 628 gr. at 244 fps
628/15432=.041 kilogram
244*.305=74.42 m/s
.5x.041*74.54^2=113.90 Joules
113.90*.738=k.e.
k.e. = 84.05 ft lbs
Now that we have done this the hard way let’s look at the easy way. First we need the constant
225,400 = The constant accounts for the arrow’s weight in grains and factors in the
pull of gravity for momentum
450,800 = The constant accounts for the arrow’s weight in grains and factors in the
pull of gravity for k.e.
Since we have a constant we can look at the formulas for momentum and k.e.
Momentum = m*v/225,400
Kinetic = m*v^2/450,800
Let’s use the arrow weight and velocity from the above example to calculate using
the much easier formulas:
Momentum = 429*287/225400 =.546 slug-ft/sec
Momentum = 628*244/225400 =.679 slug-ft/sec
Kinetic = 429*287*287/450800 = 78.38 ft lbs
Kinetic = 628*244*244/450800 = 82.94 ft lbs
Okay we now know how to calculate for momentum and k.e. What does this
mean and how do we use it in the archery world?
All manufacturers list the Kinetic Energy their bows develop. It’s all done at
the IBO rating. The standard 350 gr. arrow at X fps at 30 inch draw and 70 lbs
draw weight. This unit of measurement [k.e.] at this point has nothing to do with
penetration. They are showing you the efficiency of the bow and how well it
applies the energy to the arrow.
Kinetic Energy is just what it states, its energy. The energy is in all moving
objects. Kinetic Energy is a energy with no direction. So on impact the energy is
dispersed 360 degrees. This is not how arrows kill animals. Animals are killed by
a broad-head cutting as it moves through the animal.
Then there is momentum. Momentum is a force that drives the arrow
through the animal after impact. Since momentum is measured in slugs, slugs is the
unit of measurement showing you an amount of force in one specific direction.
This force is also in all moving objects.
An arrow is traveling in one direction and we need the arrow to travel
through the animal while cutting. We need a unit of measurement that gives us this
ability. Slugs is this unit of measurement.
I cannot tell you why the archery world uses kinetic energy instead of the
correct unit of measurement [slugs] to show penetration potential. Maybe it’s just
for simplicity reasons. Maybe it’s because it’s a larger number and we can relate to
this better I don’t know.
Look at what they say we need just for medium size game. 25-41 ft-lbs. That
is a pretty wide range there. Why is it such a wide range. Well that comes to all the
variables we have to deal with. Resistance due to type of broad-heads we use. Size
of the shafts, distance we are shooting. The resistance of the animal.
If we look at a 40 lb. bow shooting a IBO arrow of 200 gr. This arrow would
have to be at 238fps to have 25 ft-lbs of energy. This is minimum. (Now this
doesn’t take into account resistance of broad-head or distance shot or the type of
animal.) The momentum of this arrow would be .211 slug-ft/s. So since the archery
world is saying we only need 25 ft-lbs of kinetic energy, that also means we only
need .211 slug-ft/s of momentum to harvest a medium size deer. I choose 40 lb. as
the minimum draw weight. My opinion is this would be the minimum I would
recommend for hunting medium size game.
Let’s look at what happens when using the same 40 lb. bow and keeping the
kinetic energy at 25ft-lbs. Physics shows us that as mass increases, the mass
penetrates better, but how can mass penetrate better if the kinetic energy never
changes.
Let’s look at this. We saw that a 200 gr. arrow at 238 fps gave is 25 ft/lbs
kinetic energy and it gives us a momentum of .211 slug-ft/s. What happens if we
increase the weight but left kinetic energy the same. Take a 250 gr. arrow at 212
fps. We still have 25 ft/lbs of kinetic energy. So how can this arrow out penetrate if
all other factors are the same? We look at momentum. The 250 gr. arrow now has a
momentum of .235 slug-ft/s. Let’s take it one step forward. Say we use a 300 gr.
arrow. This arrow only needs to be traveling 195 fps. We still have 25 ft/lb. of
energy, but our momentum is now .260 slug-ft/s.
What does this show? By increasing the weight of this arrow being shot at
40 lb. draw weight the arrow now has a 23% increase in penetration potential. This
is why when building your hunting arrow we need to look and understand what
unit of measurement to use.
Slugs are the units of measurement we need for hunting with a bow
The kinetic vs momentum debate will always be there. The archery world
controls the market. Kinetic numbers are big numbers so in the eyes of the public it
appears to be better.
What we need to remember if nothing else, is physics never lies. A heavy
arrow will outperform a light arrow, even if the kinetic energy number is the same
between the lighter vs heavier arrow (when all other factors are equal).
As archers we need to learn what we need to look at when we decide to hunt
with a bow. Kinetic energy is the principle to show how efficient the bow applies
energy to the arrow. Momentum is the principle to show the amount of force
needed to penetrate.
I gave some examples leaving the arrow with same ke to show why arrows
that go up in weight, momentum goes up. But what really happens when adding
weight to an arrow being shot the ke also increases.
Here are two examples:
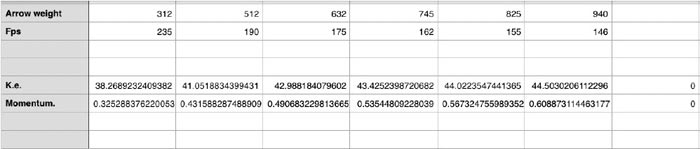
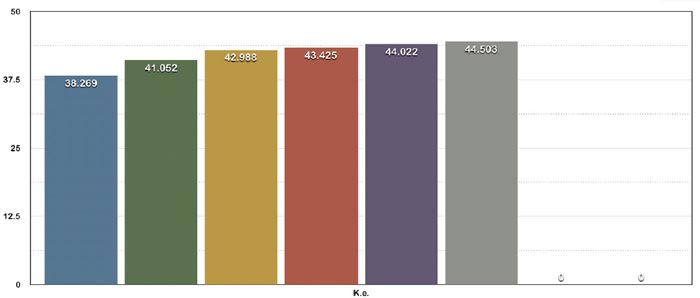
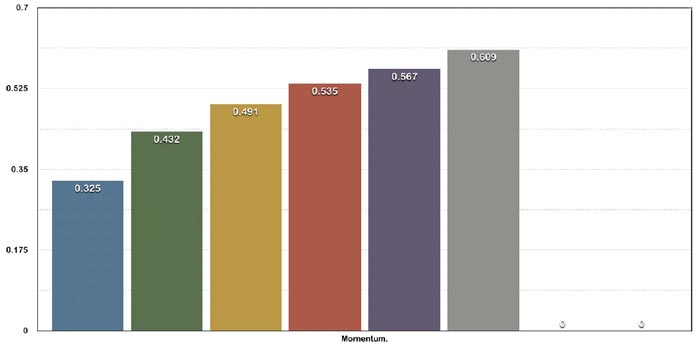
Example 1 was shot and tested from an ELITE SPIRIT at 42 lb with a 26 in draw.
Example 2 was shot and tested from an APA M 5 at 70 lb with a 26.75 draw.
Example 1:
Example 2
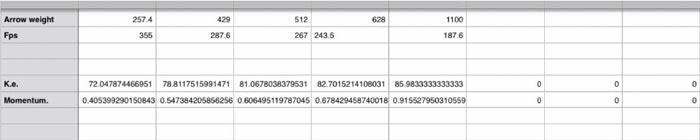
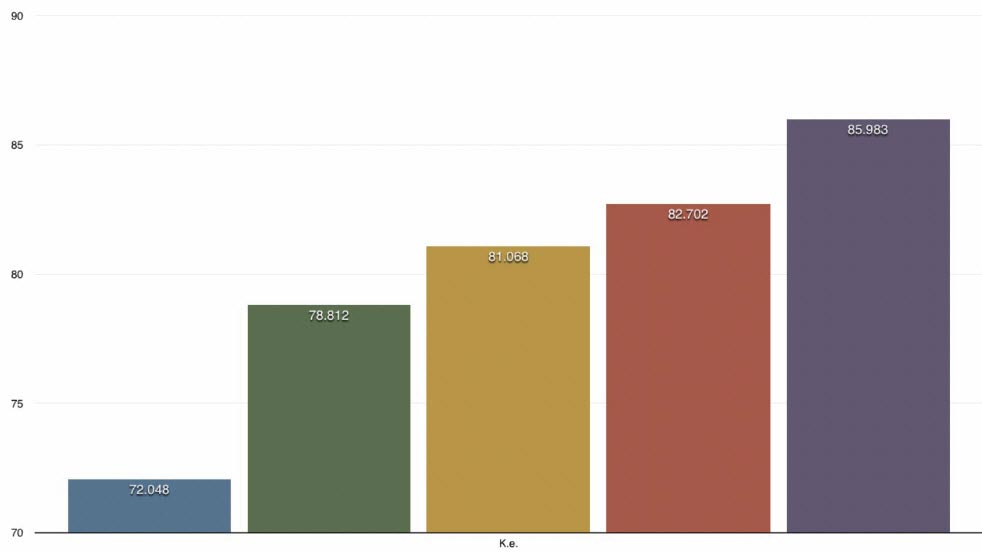
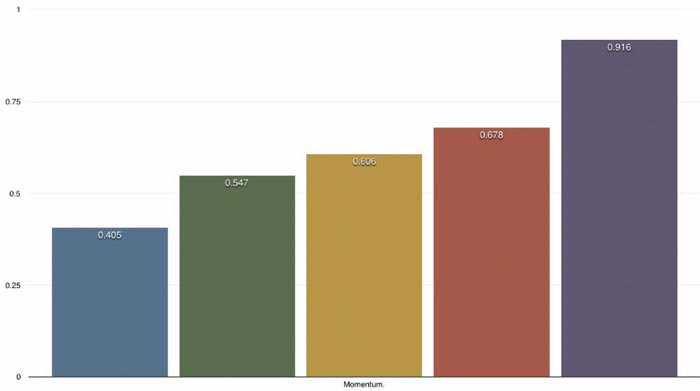
As you can see from the data ke and momentum increase as weight goes up.
The data given in example 1 was shot by hand and with a lab radar. Example 2 was
shot with a hooter shooter through a chrony chronograph at 3 ft from arrow at full
draw.
Data provided by:
Eric Newman
Rob Hummel
2017 EWN
REV. 1 – 10/21/17
